GMLscripts.com

D3D Transformations is a functionality which allows you to geometrically manipulate the points defining the structure of models, 3D shapes, primitives, and even sprites and backgrounds.  Since Game Maker is built off of Direct3D, everything drawn is defined as a set of points to be rendered.  For example, when drawing a sprite, Game Maker defines the 4 corners of the sprite that will be drawn.  Using transforms, you can rotate, scale, and move (translate) the points as much as you want.  And because they are passed through a transform matrix anyway (usually just an identity transform which does nothing to the vertices), you will experience no slowdown other than the slight overhead of defining the transforms.

There are three different types of transformations you can perform:

d3d_transform_set_translation(xt,yt,zt)   Sets the translation over the indicated vector.

d3d_transform_add_translation(xt,yt,zt)   Adds a translation over the indicated vector.

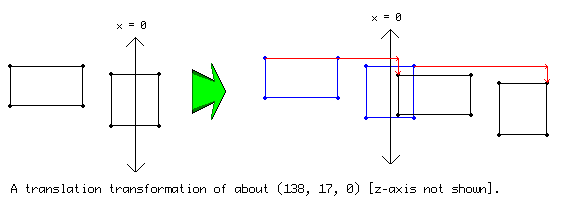
Translation: a translation transform will take the vertices used for drawing and simply add whatever coordinates you want to them.  The effect you get will effectively look like you took the object and simply moved it.

d3d_transform_set_scaling(xs,ys,zs)   Sets the transformation to a scaling with the indicated amounts.

d3d_transform_add_scaling(xs,ys,zs)   Adds a transformation to a scaling with the indicated amounts.

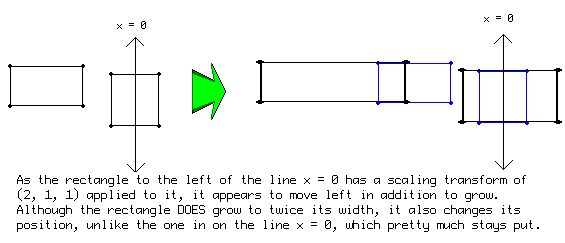
Scaling: a scaling transform will squish and expand the vertices about the various axis.  For example, a transform of d3d_transform_set_scaling( 1, 2, 0); will keep the same x coordinates, double the y coordinates and will all have the z coordinate of 0. 

NOTE:  For each axis, scaling is done about the line x/y/z = 0.  So objects that are not on this line appear to move in addition to grow.

d3d_transform_set_rotation_x(angle)   Sets the transformation to a rotation around the x-axis with the indicated amount.

d3d_transform_set_rotation_y(angle)   Sets the transformation to a rotation around the y-axis with the indicated amount.

d3d_transform_set_rotation_z(angle)   Sets the transformation to a rotation around the z-axis with the indicated amount.

d3d_transform_set_rotation_axis(xa,ya,za,angle)   Sets the transformation to a rotation around the axis indicated by the vector with the indicated amount. d3d_transform_add_translation(xt,yt,zt)

d3d_transform_add_rotation_x(angle)   Adds a transformation to a rotation around the x-axis with the indicated amount.

d3d_transform_add_rotation_y(angle)   Adds a transformation to a rotation around the y-axis with the indicated amount.

d3d_transform_add_rotation_z(angle)   Adds a transformation to a rotation around the z-axis with the indicated amount.

d3d_transform_add_rotation_axis(xa,ya,za,angle)   Adds a transformation to a rotation around the axis indicated by the vector with the indicated amount. d3d_transform_add_translation(xt,yt,zt)

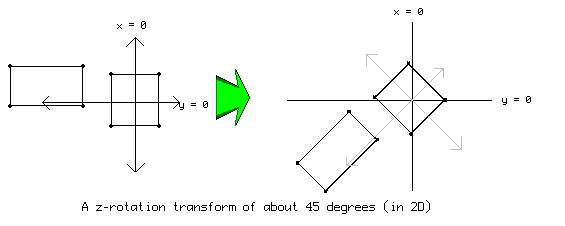
Rotation: there are three different type of rotation transforms, but the principle is the same in all three.  The coordinates are rotated about a given axis.  Imagine taking a pencil attached to a piece of paper or a 3D object like an apple.  As you twist the pencil (assuming it's sufficiently stuck in the object), you will see the effect that rotating about the axis the pencil represents will give you.  For example, if you want to rotate 2D coordinates the way we normally do, you want to (perhaps counter-intuitively) rotate about the z-axis which can be thought as pointing towards you in a 2D game.

NOTE: Like in scaling, rotation is done about the point (0,0,0).  That means objects which are not on this point will appear to move as they rotate.

The x and y rotations are similar to the z rotation, but they have less meaning in 2D (they'll just be trigonometric scaling assuming perspective is turned off).  Playing around with these in 3D, it should be fairly obvious how they work.

The last rotation transform might warrant a bit more explanation.  In the axis rotation, you define the axis you want them to rotate arround in addition to how many degrees you want them to rotate around that axis.  Imagine a globe revolving arround its axis.  The axis it's being rotated around is define as the vertex from the center of the globe to the point outside which the globe is affixed to whatever it rotates inside.

d3d_transform_set_identity()   Sets the transformation to the identity (no transformation).

Transforms effect everything that is drawn after the transform is set, including sprites/backgrounds and 2D shapes in addition to anything 3D.  So after you draw everything you want drawn, remember to call d3d_transform_set_identity(); so that everything else is drawn normally.  For example, drawing a sprite at 0,0 rotated 45 degrees then a sprite at 100,0 not rotated at all:

Expand{
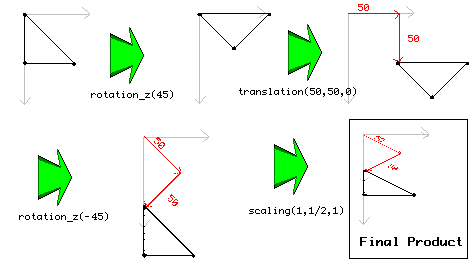
    d3d_transform_set_rotation_z( 45);
    draw_sprite(spr,0,0,0);
    d3d_transform_set_identity();
    draw_sprite(spr2,0,100,0);
}

The difference between the d3d_transform_add_*** and the d3d_transform_set_*** is that d3d_transform_set_*** will clear all the transforms before it, where the d3d_transform_add_** "adds" the new transform to the old ones.  What does it mean to add a transform onto an old one?  Well, imagine if you could only apply one transform to whatever shape you wanted.  This would be mighty inconvenient because anything you wanted rotated would either have to appear at (0,0,0) or would be some crazy place you can't predict.  So what you do is you apply a rotation to the object THEN a translation to the object so that it will be rotated about the point (0,0,0) and then will be moved to the correct place.

Expand{
    d3d_transform_set_identity();
    d3d_transform_add_rotation_z(45);
    d3d_transform_add_translation(100,100,0);
    draw_sprite(spr,0,0,0);
    d3d_transform_set_identity();
}

How on earth can you keep track of what cascading transforms will accomplish and how to logically justify what happens to them?  Well, you have to start with the end.  That is to say, you start by imagining (or drawing) where the points that are drawn in the draw statement after all the transforms.  Then, one-by-one, apply the next transform you defined to the points you end up with from the previous transform. 

For example, in the following code:

Expand{
    d3d_transform_set_identity();
    d3d_transform_add_rotation_z(45);
    d3d_transform_add_translation(50,50,0);
    d3d_transform_add_rotation_z(-45);
    d3d_transform_add_scaling(1,1/2,1);
    draw_triangle(0,0,0,50,50,50,1);
    d3d_transform_set_identity();
}

You start with the coordinates of the triangle and then one-by-one apply the transforms:

As you can see, transforms can be used both in 2D and in 3D.  Even though you can think of them as a series of actions on each and every vertex, the fact is all these actions are stored on a single fixed-size matrix (through matrix multiplication) and so you shouldn't expect lag from drawing an object after you applied thousands of transforms to it.  The following functions can help you build such a stack without having to have it always applied to everything drawn.  They create ways of storing the current transformation so you can get rid of it and use it later.  They also work great for hierarchical structures.

d3d_transform_stack_clear()   Clears the stack of transformations.

d3d_transform_stack_empty()   Returns whether the transformation stack is empty.

d3d_transform_stack_push()   Pushes the current transformation on the stack. Returns whether there was room on the stack to push it there (if you forget popping transformation you at some moment will run out of room on the stack).

d3d_transform_stack_pop()   Pops the top transformation from the stack and makes it the current one. Returns whether there was a transformation on the stack.

d3d_transform_stack_top()   Makes the top transformation the current one, but does not remove it from the stack. Returns whether there was a transformation on the stack.

d3d_transform_stack_discard()   Removes the top transformation from the stack but does not make it the current one. Returns whether there was a transformation on the stack.

Make sure you don't create an infinitely-growing stack, or create a stack underflow by popping a stack that's empty.

One use of the d3d_transform_stack functions that makes use of this ever-growing series of transforms things is an easy way to get "perfect" ball rotation.  This only works for one ball at a time, but in the create event, push a normal identity transform and then in the draw event, apply an axis rotation to the already-rotated vertices:

Expand{
    d3d_transform_stack_pop();
    d3d_transform_add_rotation_axis( -vy, vx, 0, dist * 2.3);
    d3d_transform_stack_push();
    
    d3d_transform_add_translation( x, y, z);
    d3d_draw_ellipsoid( - 0.5, - 0.5, - 0.5, 0.5, 0.5, 0.5, 0, 1, 1, 8);
    d3d_transform_set_identity();
}

The transform stack will memorize the previous rotation of the ball so that it's a simple matter of applying the new rotation and then memorizing it.  Remember, you have to make sure the translation is outside of that stack because when you rotate an object that is translated so that it is not centered at the point (0,0,0), crazy things happen.

Well, that's my knowledge of transformed, I hope this helps you understand this powerful tool built into the engine GM's built off of.  Here's hoping Game Maker has more transform functionallity in the future.  In particular better ways of storing more matrix transforms and ways of applying the various transforms in the other direction in the future (which'd make heirarchical constructions a whole lot easier).

-EyeGuy